2進数とは?なぜ使う?|10進数からの簡単な変換方法(小数含む)
コンピュータの中で数字ってどのように表されているか知っていますか?
実は0と1だけで表現されているんです。
今回の記事ではIT入門編ということで、電気を数字で表す方法の2進数について解説します。
プログラミングしかしないから知らなくてもいい…なんてことはなく、コンピュータを使って作業をするのであれば知っていて損はない基礎知識です。
分かりやすく解説しますので、一緒に理解を深めましょう!
- 2進数とは?
- なぜ2進数が使われているのか?
- 2進数から10進数への変換方法
- 10進数から2進数への変換方法
解説動画
今回の記事はこちらの動画をまとめたものです。
2進数とは?基本知識
まずは2進数がどんなものなのかを理解しましょう。
普段使っている数字は10進数
私たちが普段何気なく使っている数字は10進数と言います。
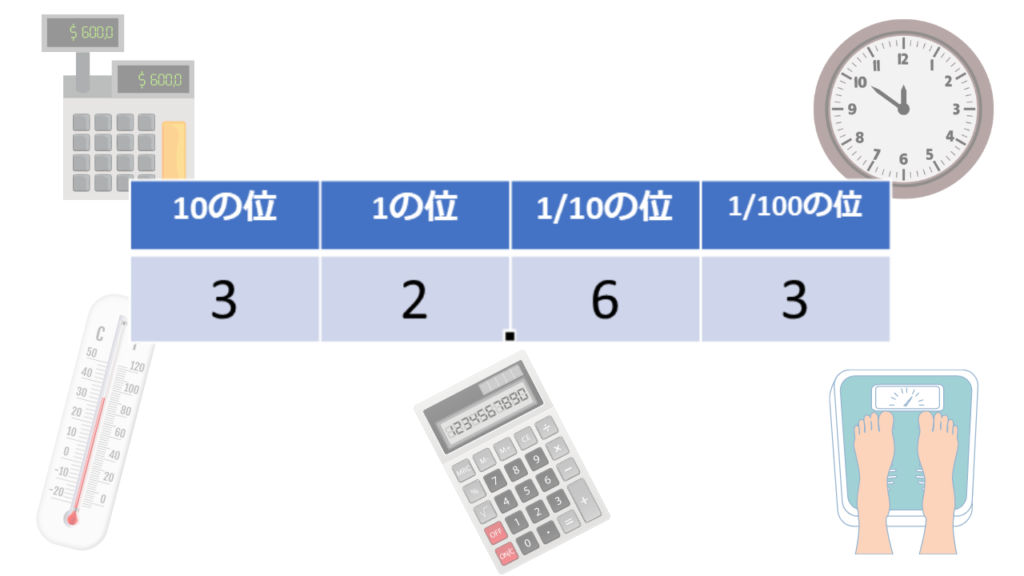
10の位、1の位、1/10の位、1/100の位…それぞれの位が10ごとにあります。
1つの位に、0~9の10パターンの数字を入れて表現しています。
2進数
コンピュータで使われるのは10進数ではなく2進数です。
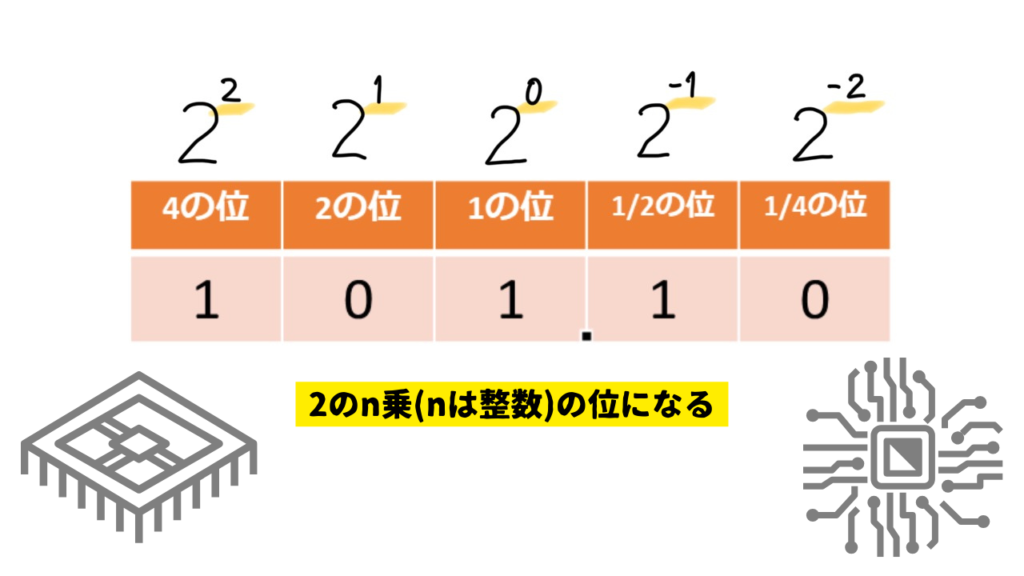
4の位、2の位、1の位、1/2の位、1/4の位…それぞれの位が2のn乗で表現されます。
1つの位に、0か1の2パターンの数字を入れて表現しています。
つまり、
これが2進数です。
なぜコンピュータの中で2進数が使われるのか
なぜコンピュータの中で10進数を使わず2進数を使うのでしょうか。
それは
1.数値を電気的に表現でき
2.半導体を使って電気的に計算できる
からなんです。
数値を電気的に表現する方法
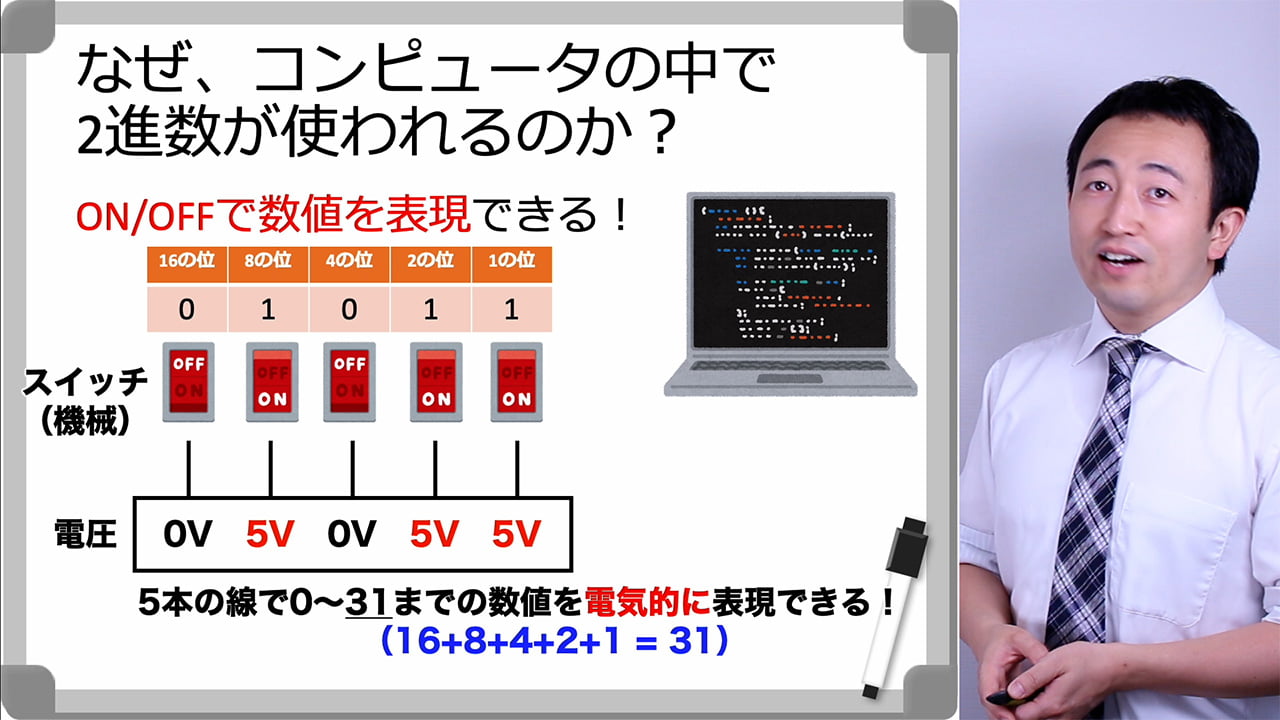
ON/OFFのできるスイッチ(機械)があったとします。
スイッチのOFFを0、ONを1とすると…
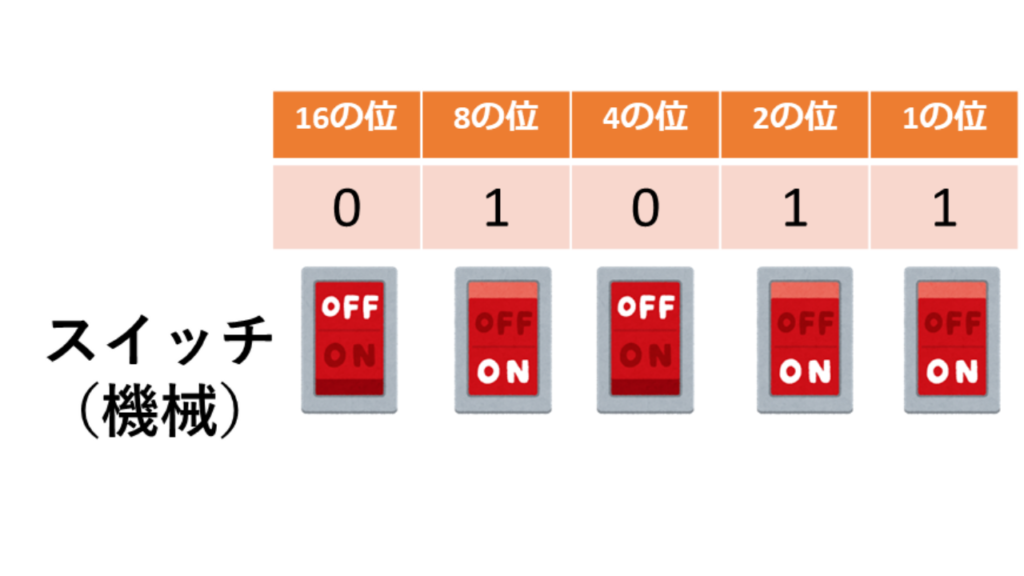
このような表現ができます。
OFF、ON、OFF、ON、ONで01011と表せちゃうんです。

な、なんだそれ…
さらにスイッチに回路を繋げて、OFFを0V、ONを5Vとしましょう。
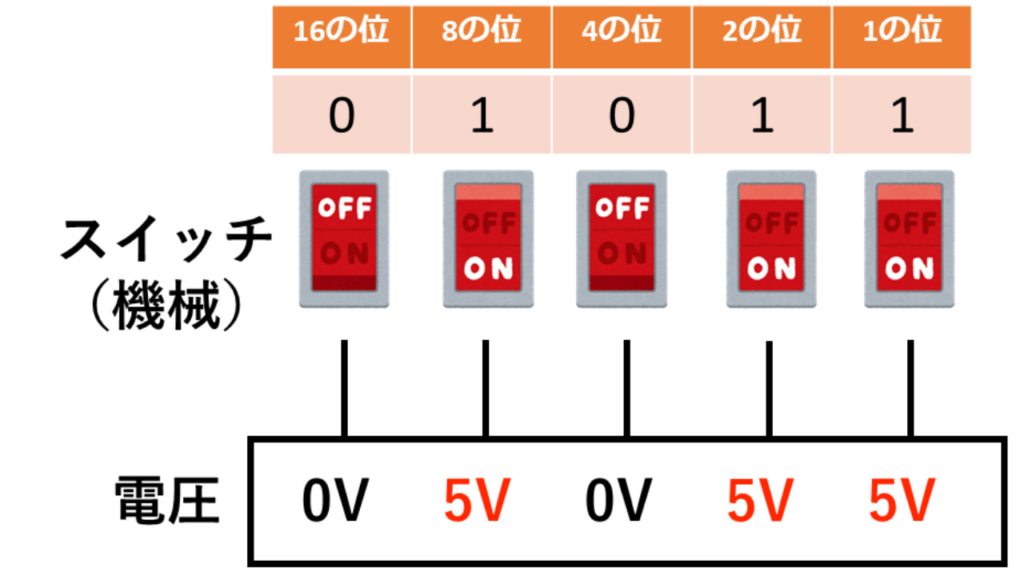
すると0V、5V、0V、5V、5Vで01011と表せます。
5本の線で0~31までの数値を電気的に表現することができるんです。

そうか、電気は話せないから
ON/OFFで伝えるしかないのか!
半導体を使って電気的に自動計算する方法
ではその0と1で表された2進数はどのように計算をしているのでしょう。
それは半導体を使って計算しているんです。
半導体素子と言われるパーツが計算をしてくれるんですよ。
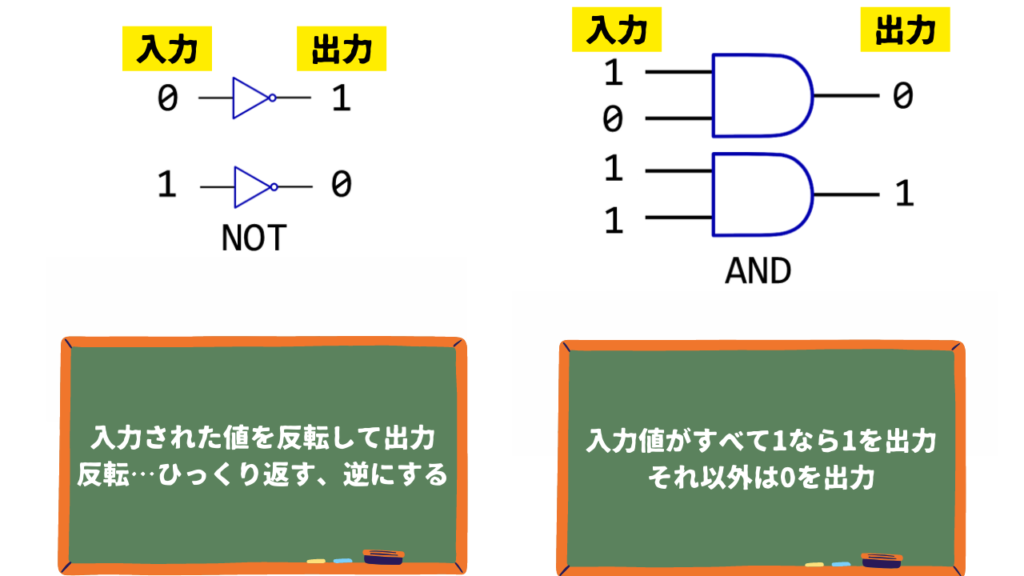

NOTやANDが何になるんだ…
これ1個じゃ何だそれってなります(笑)
でも組み合わせれば計算できるようになります!
2進数の計算例:1桁の足し算
2進数の1桁の足し算は4パターンしかありません。
足す数、足される数をそれぞれA、Bとします。
また答えの2桁目(桁上がり)をC、1桁目(合計)をSとします。
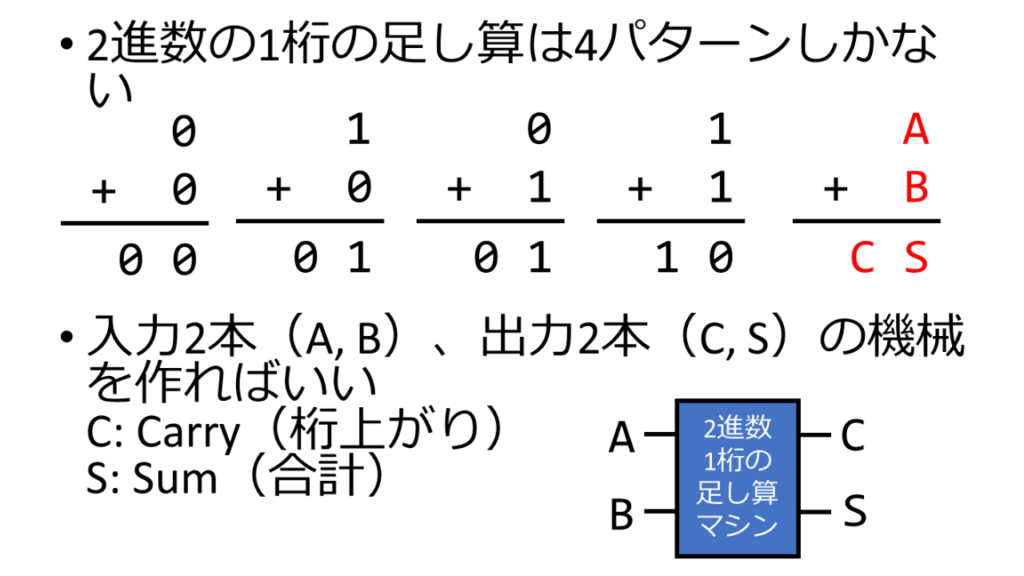
これを機械化すると、入力のAとBの2本の線がマシンに入り、出力のCとSの2本の線がマシンから出てくるイメージです。
このマシン内に先ほどの半導体素子と言われるパーツを入れて設計すればいいのです。
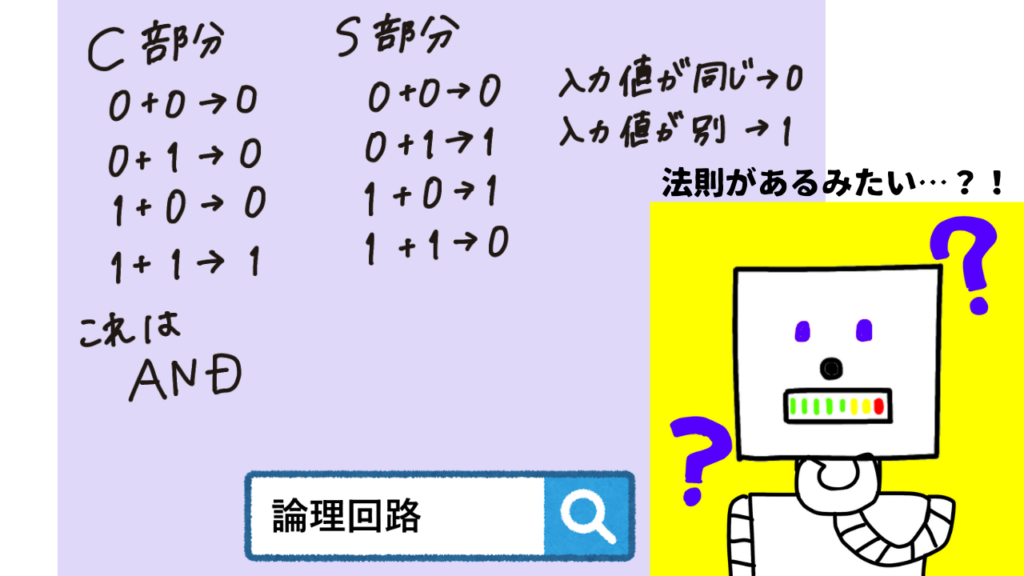
実際どのような回路になるかは難しくなるので省略します。
気になる方は論理回路などで検索して勉強してみてください!
もちろん、足し算だけでなく、引き算、かけ算、わり算…と計算ができます。
それをぎゅーっとつめて小さくまとめたやつがCPUです。
コンピュータの脳みそです!
以上、コンピュータで2進数を使う理由について解説しました。
1.数値を電気的に表現でき
2.半導体を使って電気的に計算できる
というのが理解できたでしょうか?
2進数から10進数に変換する方法
2進数を10進数に変換してみましょう。
例えば10110100で表された2進数。
128の位は存在する、32の位は存在する、16の位は存在する、4の位は存在する…と1がある位を足します。
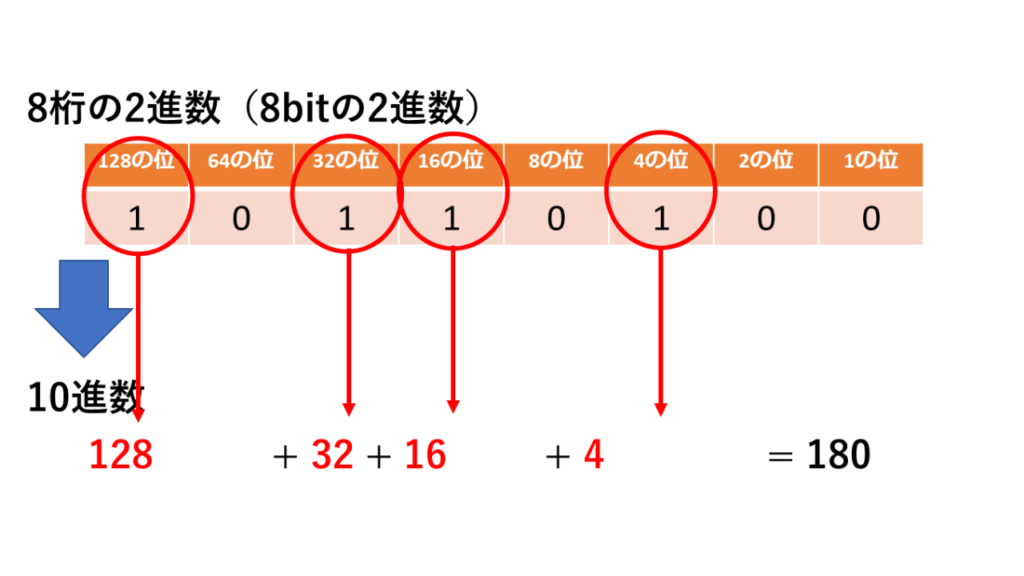
すると128+32+16+4=180で10進数に変換することができます。
1がある位が何の位か分かれば、簡単に変換できます!
小数も同じように2進数から10進数に変換できる
もちろん小数の場合も同じように変換できます。
8の位、1の位、1/4の位、1/16の位…と1がある位を足します。
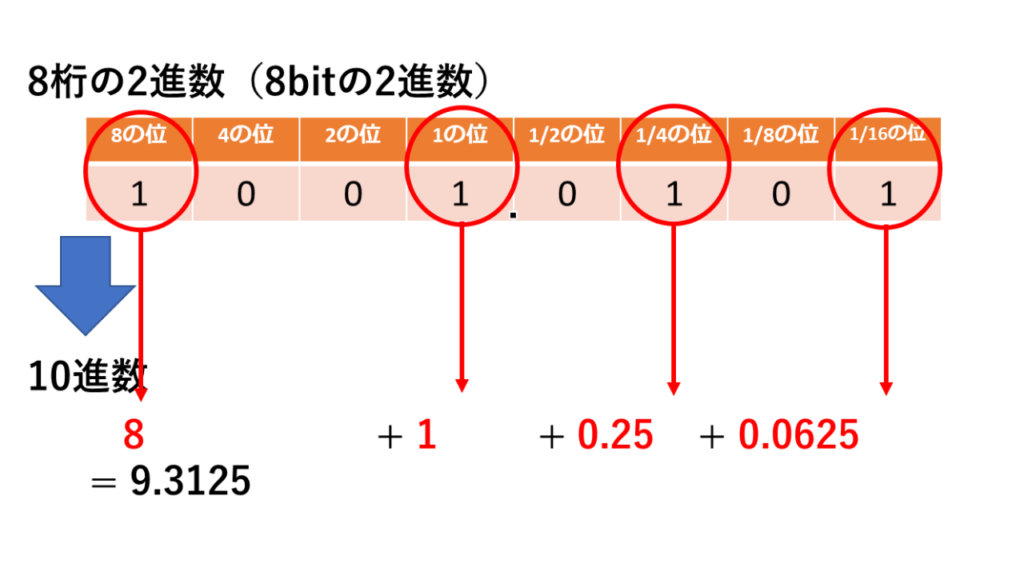
8+1+0.25+0.0625=9.3125と10進数に変換できました。
10進数から2進数に変換する方法
10進数を2進数に変換してみましょう。
先ほどの2進数から10進数に変換する方法と逆のことをしていきます。
10進数で122という数字、8桁の2進数に変換します。
128の位の128と比べると、122の方が小さいので、128の位は0です。
次に64の位の64と比べると、122の方が大きいので、64の位は1です。
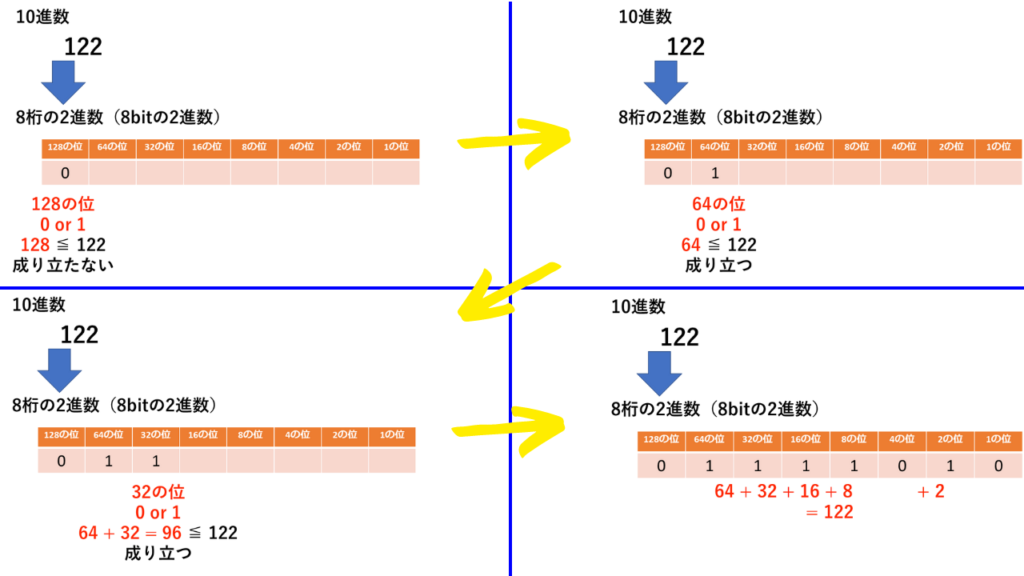
32の位の32と比べると、(先ほど1が入った)64+32=96で122の方が大きいので、32の位は1です。
・・・と上位の位から、1が入る位のみ足して122を超さないか比較し、1または0を入れていくと2進数に変換できます。
10進数の122は2進数では01111010となります。

これ結構大変だよ…
もうちょっと機械的にできる方法を解説します!
10進数から2進数に簡単に変換する方法
変換したい10進数を2で割っていく方法です。
122÷2=61あまり0、61÷2=30あまり1、30÷2=15あまり0…とどんどん割ります。
商(割り算の答え)が0になったところで終わります。
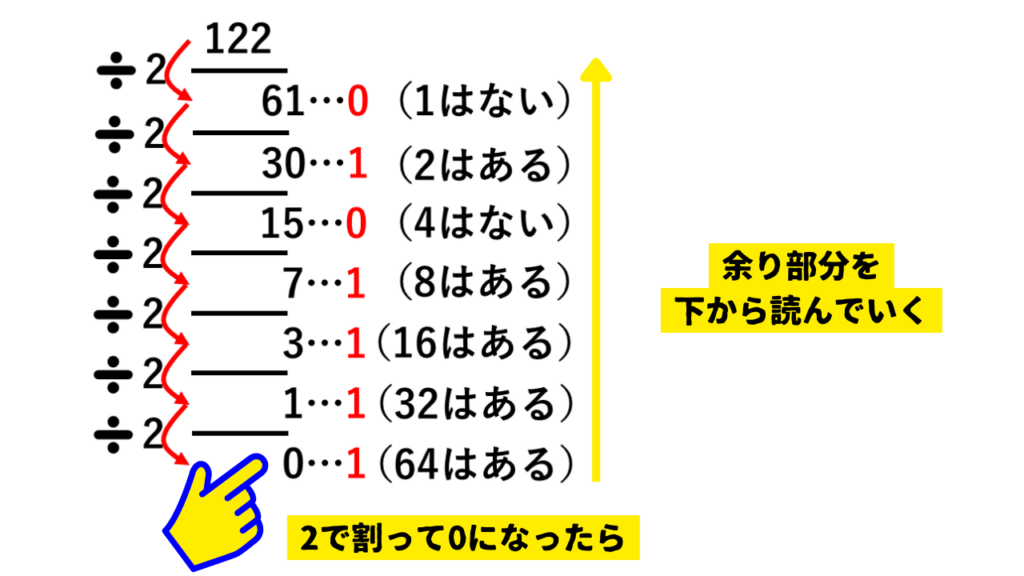
最後に余り部分を下から読み上げて、1111010つまり8桁だと01111010となります。

どうして下からなの?
最初の122÷2=61あまり0は、(あまり0なので)1の位はないという意味です。
次の61÷2=30あまり1は、(あまり1なので)2の位はある、
その次の30÷2=15あまり0は、(あまり0なので)4の位はない…となっているのです。
小数も10進数から2進数に変換できる
まずは変換したい10進数を、整数と小数にわけます。
分けたあとは整数のみの10進数から2進数への変換方法と同じです。
1/2の位の0.5と比べると、0.25の方が小さいので、1/2の位は0です。
次に1/4の位の0.25と比べると、0.25と同じなので、1/4の位は1になります。
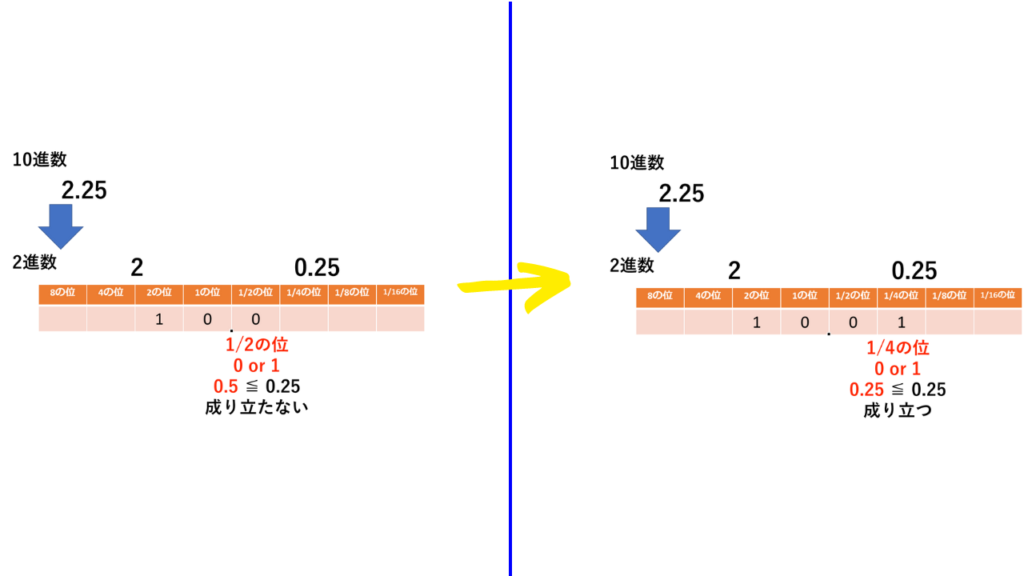
比較する値同士が同じになったので終わります。
つまり2.25という10進数は、10.01という2進数で表されます。

これも簡単な方法ある?
小数の場合は、2倍していく方法があります。

0.25の場合は、0.25×2=0.5で1/2の位は0、
0.5×2=1.0で1/4の位は1です。
小数点以下のみ2倍していきますので、小数点以下が0になるとそこで終わります。
2進数の場合、ほとんどの小数は誤差を含んでいる
0.25では簡単だったので、0.3を2進数に変換していきましょう。
0.3×2=0.6、0.6×2=1.2、(小数部分のみ2倍するので)0.2×2=0.4、
0.4×2=0.8、0.8×2=1.6、(小数部分のみ2倍するので)0.6×2=1.2、、、

気付いたでしょうか。
これずっと続いてしまうのです。
つまり0.3を2進数にすると0.01001100・・・
もし小数点以下8桁で切り捨てると、0.01001100となり、再度10進数に変換すると
0.25+0.03125+0.015625=0.296875となります。
つまり、ほとんどの2進数で表される小数は誤差を含んでいる、ということになります。
プログラミングをするときはこのことに気を付けなくてはなりません。
誤差として±1%にしたり
ある数値になったら→ある数値を超えたらにしたり
工夫してプログラミングをします!
まとめ
今回の記事では、コンピュータの中で使われている2進数について解説しました。
- 2進数とは?
- なぜ2進数が使われているのか?
- 2進数から10進数への変換方法
- 10進数から2進数への変換方法
とくに0.3が誤差を含むということは、驚いた方も多いのではないでしょうか。
コンピュータにも苦手なことがあるんですね!
2進数について学んだけど、ロボット作りはまだ先でいいかな…と後回しにしていませんか?
電子工作やロボット作りを始めるなら、豆電球回路から始めることをおすすめしています。
これなら簡単に始められるので、最初の一歩を踏み出しましょう!

最後まで読んでいただき、ありがとうございました!
以上、CHAでした!

